【力学】慣性モーメントは座標変換してから求めるべし

剛体の力学では、回転による運動方程式を作るために軸まわりの慣性モーメントを計算する問題がよく出ます。ですが、編入生がよく使う基礎物理学演習や演習力学などで紹介されている慣性モーメントの求め方は、球や円柱の慣性モーメントを計算するために円盤の慣性モーメントが必要で、円盤の慣性モーメントを求める場合でも少し複雑な計算をしなければなりません。実際、慣性モーメントは覚えておくのも手ではあるのですが、慣性モーメントを求めるという問題が出た場合はしっかりと途中計算をしなければいけなく、とても面倒です。
今回はそのような円、球などの物体に適切な座標変換を施して比較的簡単に慣性モーメントを求める方法を紹介します。

準備

慣性モーメントの定義

まず始めに慣性モーメントの定義から確認していこうと思います。慣性モーメントの定義は微分によるものと積分によるものがあると思いますが、微分によるものを挙げて話を始めたいと思います。

質量 $dm$ の質点のある軸まわりの慣性モーメント $dI$ とは、軸と質点との距離を $r$ とすると

$\begin{align}dI=r^2dm \end{align}$

で表される量のことである。

デカルト座標系と慣性モーメント

次にデカルト座標系*1の各座標軸まわりの慣性モーメントの式を慣性モーメントの定義式から導出します。
先に注意しておきますが、定義式における $r$ は軸からの距離です。これについては慣性モーメントの物理的な意味を理解していれば全く問題無いのですが、重心からの位置と混同しないように注意しましょう。

定義式では質点を考えていましたが、質点は微小な体積の物体とみなしてもよいと考えます。質点の位置を $\boldsymbol{x}$ とし、その物体の体積を $dV$ 、体積密度*2を $\rho(\boldsymbol{x})$ とすると*3

$dm=\rho(\boldsymbol{x})dV$

と表せます。次に、質点の座標を $P(x, y, z)$ とすると、三平方の定理より $P$ の $x$ 軸との距離 $r_x$ は

$r_x=\sqrt{y^2+z^2}$

同様に、 $y$ 軸からの距離 $r_y$ は

$r_y=\sqrt{x^2+z^2}$

$z$ 軸からの距離 $r_z$ は

$r_z = \sqrt{x^2+y^2}$

となるから、これらを慣性モーメントの定義に代入して物体全体で積分すると、各座標軸まわりの慣性モーメントは

$I_x=\displaystyle \iiint_D \rho(\boldsymbol{x})(y^2+z^2)\ dV$

$I_y=\displaystyle \iiint_D \rho(\boldsymbol{x})(x^2+z^2)\ dV$

$I_z=\displaystyle \iiint_D \rho(\boldsymbol{x})(x^2+y^2)\ dV$

と表され、 $I_x$ を $x$ 軸まわりの慣性モーメントといいます*4。ここで積分領域である $D$ は慣性モーメントを求める物体の領域です。すなわち半径が $a$ の球であれば

$D=\left\{(x, y, z)\ | \ x^2+y^2+z^2 \leq a^2 \right\}$

になります。

座標変換と慣性モーメント

球の中心を通る軸まわりの慣性モーメント

ここから本題に入りますが、まず始めに半径 $a$ で全質量が一様に $M$ の球の中心を通る軸まわりの慣性モーメントを求めてみたいと思います。準備としては、先程導出したデカルト座標系における $z$ 軸まわりの慣性モーメントの式を使いたいので以下のように仮想的に座標軸を設置します。（この考え方が重要）
f:id:yoshi12030:20180630094616p:plain
ここでは、 $z$ 軸まわりの慣性モーメントの式を使いますが、上図のように球を設置したときは、球の対称性から $x$ 軸まわりの慣性モーメントや $y$ 軸まわりの慣性モーメントを使っても構いません。
次にデカルト座標系から3次元極座標系（球面座標系）へ座標変換します。すなわち

$x=r\sin \theta \cos \varphi$
$y=r\sin \theta \sin \varphi$
$z=r\cos \theta$

とおきます。この座標変換のヤコビアン $J$ は

$J=r^2\sin \theta$

となります。すなわち

$dV=dxdydz=r^2\sin \theta drd\theta d\varphi$

のようになります。このようにすれば後は計算するだけで良いです。球の体積密度は物体全体で一様で $\displaystyle \rho=\frac{M}{\frac{4}{3}\pi a^3}$ となるので

$\begin{align}I_z &= \displaystyle \iiint_D \rho \ (x^2+y^2)dV \\ &= \displaystyle \frac{M}{\frac{4}{3}\pi a^3} \iiint_{D'} r^2 \sin^{2} \theta \times r^2\sin \theta\ drd\theta d\varphi \\ &= \displaystyle \frac{M}{\frac{4}{3}\pi a^3} \int_0^a r^4 dr \int_0^{\pi} \sin^{3} \theta d\theta \int_0^{2\pi} d\varphi \\ &= \displaystyle \frac{M}{\frac{4}{3}\pi a^3} \left[\frac{1}{5}r^5\right]_0^a \ 2\times \int_0^{\frac{\pi}{2}} \sin^{3} \theta d\theta \ \Bigl[\ \varphi \ \Bigr]_0^{2\pi} \\ &= \displaystyle \frac{M}{\frac{4}{3}\pi a^3} \times \frac{1}{5}a^5 \times 2 \times \frac{2}{3} \times 2\pi \\ &= \displaystyle \frac{2}{5}Ma^2 \end{align}$

のように求まります。3行目から4行目への変形は $\sin^{3} \theta$ が $\theta = \displaystyle \frac{\pi}{2}$ で左右対称であることを利用しています。（グラフを書けば分かる）
また、4行目から5行目への変形はウォリスの積分公式

$\displaystyle \int_0^{\tfrac{\pi}{2}} \sin^n \theta \, d\theta =\int_0^{\tfrac{\pi}{2}} \cos^n \theta \, d\theta =\begin{cases}\displaystyle \frac{n-1}{n} \cdot \frac{n-3}{n-2} \cdots \frac{2}{3} \cdot 1 & (n=2k-1) \\ \\ \displaystyle \frac{n-1}{n} \cdot \frac{n-3}{n-2} \cdots \frac{1}{2} \cdot \frac{\pi}{2} & (n=2k) \end{cases}$

（ただし $k$ は自然数）を使いました。このように計算すれば、わざわざ円盤の慣性モーメントを求めなくても一発で慣性モーメントを求めることが出来ます。

その他の物体の慣性モーメント

前で説明した方法は円柱や円盤の慣性モーメントを求めるときにも使えます。円柱の場合は円柱座標への座標変換、円盤の場合は2次元極座標への座標変換を使い、それぞれ適切な密度（円盤の場合面積密度）をデカルト座標系の慣性モーメントの公式に入れ込めば良いです。これらの計算は~~面倒なので~~この記事を読んでいる方への演習問題とします。

ちなみに、円柱は以下の図で $z$ 軸まわりの慣性モーメントも求められますが、 $x$ 軸や $y$ 軸まわりの慣性モーメントも簡単に求められますので試してみて下さい。
f:id:yoshi12030:20180630112709p:plain

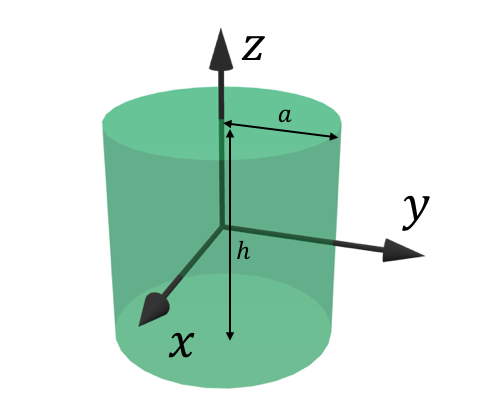
上図は、円柱の重心と原点を一致させて描いています。投げっぱなしは申し訳ないので上図の円柱の慣性モーメントのみ載せておきます。

$\displaystyle I_z=\frac{1}{2}Ma^2$

$\displaystyle I_x=I_y=\frac{M}{12}(3a^2+h^2)$

是非色々な図形で試してみて下さい。

*1:直交座標系のことである

*2:この記事では密度は全て質量密度を指す

*3:ここでは一般的な議論をしているので体積密度は位置の関数とするが、具体例では定数として扱う

*4:他の軸についても同様

ヨッシーの日記

いろいろかきます